$\nabla$ Engineering & Mathematics

Definition

In the time domain first order systems are the solution $y(t)$ of the following differential equation $$\begin{equation}\label{foDef} \begin{cases} \dfrac{dy(t)}{dt}=-\omega_0 y(t)+Gu(t) \\ y(0)=y_0 \end{cases} \end{equation}$$ where all the quantities are scalars, $y_0$ is the initial condition of $y(t)$, $u(t)$ is the input of the system and $G$ and $\omega_0$ are constants.

In the Laplace domain $\eqref{foDef}$ becomes $$\begin{equation}\label{foDefLapIni} Y(s)= H(s)U(s)+\frac{H(s)}{G}y_0, \quad \text{with} \quad H(s)= \frac{G}{s+\omega_0} \end{equation}$$ where $H(s)$ is the transfer function of $y(t)$.

From now on we will consider $y_0=0$ and under this condition $\eqref{foDefLapIni}$ becomes $$\begin{equation}\label{foDefLap} Y(s)= H(s)U(s) \end{equation}$$

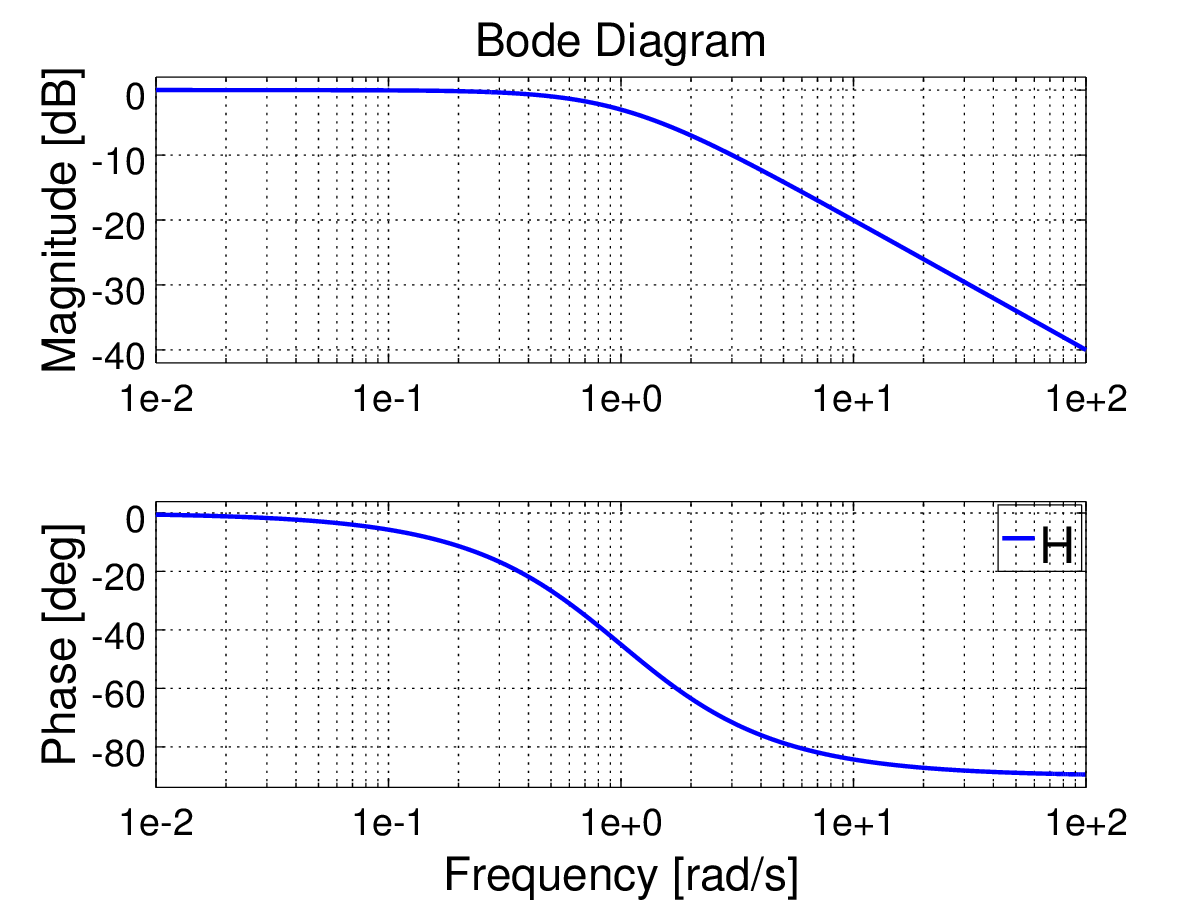
If $\omega_0 > 0$, which is usually the case for physical systems of this type, $\eqref{foDef}$ is asymptotically/BIBO stable (asymptotic and BIBO stability are equivalent for first order systems) and the time response to the step function $$u(t) = \begin{cases} 1 & \text{if } t \geq 0 \\ 0 & \text{if } t < 0 \end{cases}$$ is shown in figure 1 while figure 2 represents the Bode plot of $H(s)$.

Examples

Mechanical Domain

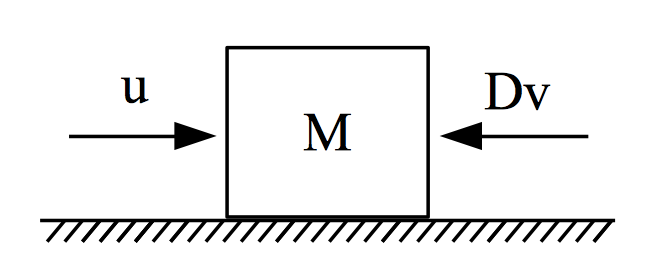
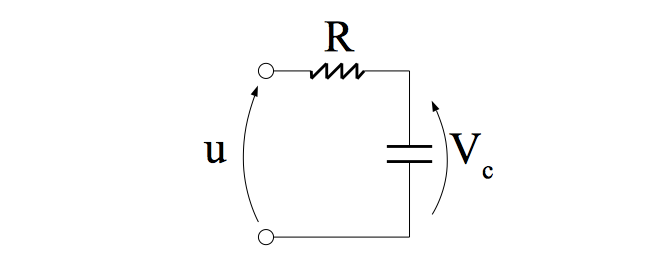
In the mechanical domain a first order system can be built using a mass force system with viscous damping, ($M$, $u$ and $D$ respectively, see figure 3). From Newton we have $$Ma=u-Dv$$ which can be represented through velocity as $$\begin{equation} \label{mechSyst} M\frac{dv}{dt}=-Dv+u \implies \frac{dv}{dt}=-\frac{D}{M}v+\frac{1}{M}u \end{equation}$$ Comparing $\eqref{mechSyst}$ with $\eqref{foDef}$ we have that for a mechanical system $y=v$, $G=\frac{1}{M}$ and $\omega_0=\frac{D}{M}$. A small note is made on $\omega_0$ which is positive implying that the system is stable.

In the Laplace domain $\eqref{mechSyst}$ becomes $$\begin{equation}\label{mecha} sMV=-DV+U \implies V=\dfrac{U}{sM+D} \implies V=\dfrac{1}{M}\frac{1}{s+\frac{D}{M}}U \end{equation}$$

Electrical Domain

In the electrical domain a first order system is represented by an RC circuit (figure 4) . Using Kirchhoff's voltage law we have $$\begin{equation}\label{eleSys} u=iR+v_c \xRightarrow{i=C\frac{dv_c}{dt}} RC\frac{dv_c}{dt}=u-v_c \implies \frac{dv_c}{dt}=-\frac{1}{RC}v_c+\frac{1}{RC} u \end{equation}$$ From Laplace we obtain $$\begin{equation}\label{electro} sV_c=-\frac{1}{RC}V_c+\frac{1}{RC}U \implies V_c=\frac{1}{RC}\frac{1}{s+\frac{1}{RC}}U \end{equation}$$ and comparing $\eqref{eleSys}$ with $\eqref{foDef}$ (or equivalently $\eqref{electro}$ with $\eqref{foDefLap}$) it can be seen that $y=v_c$, $G=\frac{1}{RC}$ and $\omega_0=\frac{1}{RC}$. A small note is made on $\omega_0$ which is positive implying that the system is stable.

Cut off frequency

Also known as corner or break frequency, the cutoff frequency decreases the energy flow through a system and obstructs it from working as intended.

The cutoff frequency of a first order system can be found by analysing the magnitude of $H(j\omega)$ (Figure 2) $$\begin{equation}\label{bodeCo} \lvert H(j\omega) \rvert =\frac{G}{\sqrt {\omega^2 +\omega^2_0}} \end{equation}$$ $\lvert H(j\omega) \rvert$ behaviour can be assessed considering that it is monotonically decreasing and it has two asymptotes, that is $$\begin{equation}\label{asy} \lvert H(j\omega) \rvert\simeq \begin{cases} H_0=\dfrac{G}{\omega_0} & \text{if } \omega \ll \omega_0 \\ H_R=\dfrac{G}{\omega} & \text{if } \omega \gg \omega_0 \end{cases} \end{equation}$$ These properties guaranty that there is a cutoff frequency and it can be calculated by finding where $H_0$ and $H_R$ intersects (from $\eqref{asy}$, $H_0$ is constant while $H_R$ is a function of $\omega$), that is $$H_0=H_R\left( \omega_c \right) \implies \frac{G}{\omega_0}=\frac{G}{\omega_c}$$ and the cutoff frequency is $$\begin{cases} \omega_c =\omega_0 & \left [ \text{rad/s} \right] \\ f_c =\dfrac{\omega_0}{2\pi} & \left [ \text{Hz} \right] \end{cases}$$ From here we can also find that $$\begin{equation} \lvert H(j\omega_c) \rvert =\frac{1}{\sqrt {2}}\frac{G}{\omega_0} \implies \lvert H(j\omega_c) \rvert =\frac{1}{\sqrt {2}} H_0 \end{equation}$$ which shows that in $\omega=\omega_c$, $\lvert H(j\omega) \rvert$ loses 3dB $\left( =20\text{log}\left( \sqrt {2} \right) \right)$.

Figure 2 shows an example where $\omega_0=1$.

For the two systems described in the above examples the cutoff frequency (Hz) is $$\begin{align} \text{Mechanical:}\quad & f_c=\frac{D}{2\pi M} \\ \text{Electrical: } \quad & f_c=\frac{1}{2\pi RC} \end{align}$$

Settling time

The settling time of $\eqref{foDef}$ can be calculated in the Laplace domain applying the step function $$u(t) = \begin{cases} 1 & \text{if } t \geq 0 \\ 0 & \text{if } t < 0 \end{cases} \xRightarrow[]{\mathscr{L}\text{ }} \frac{1}{s}$$ to $\eqref{foDefLap}$. The response becomes $$Y= \frac{G}{s(s+\omega_0)}$$ which can be written as $$Y= \frac{G}{\omega_0}\left( \dfrac{1}{s}-\frac{1}{s+\omega_0} \right)$$ and returning back to the time domain we obtain $(t\geq) 0$ $$\begin{equation}\label{tsol} y(t)=\frac{G}{\omega_0}\left(1 -e^{-\omega_0 t} \right) \end{equation}$$ Now, to find the rise time we will need the settling value of $\eqref{tsol}$ and to do this we take its limit as $$\begin{equation}\label{lim} \lim_{t\to\infty} \frac{G}{\omega_0}\left(1 -e^{-\omega_0 t} \right)=\frac{G}{\omega_0} \end{equation}$$ Defining $(t_s)$ as the time required to reach 98% of $\eqref{tsol}$'s final value then from $\eqref{tsol}$ and $\eqref{lim}$ we obtain the following equation $$0.98\frac{G}{\omega_0}=\frac{G}{\omega_0}\left(1 -e^{-\omega_0 t_s} \right) \implies 0.98=1 -e^{-\omega_0 t_s} \implies t_s = -\frac{\ln (0.02)}{\omega_0}$$ and from here we finally calculate the settling time as $$\begin{equation} t_s \simeq \frac{4}{\omega_0} \end{equation}$$ For the two systems described in the above examples the settling time is $$\begin{align} \text{Mechanical:}\quad & t_s = 4\frac{M}{D} \\ \text{Electrical: } \quad & t_s = 4RC \end{align}$$